8. Tidal Friction, Kant and Thomson-Tait on the Rotation of the Earth and Lunar Attraction
Thomson and Tait, Nat. Philos., I, p. 191 (paragraph .276):
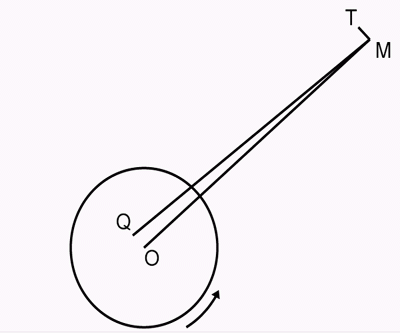
"There are also indirect resistances, owing to friction impeding the tidal motions, on all bodies which, like the earth, have portions of their free surfaces covered by liquid, which, as long as these bodies move relatively to neighbouring bodies, must keep drawing off energy from their relative motions. Thus, if we consider, in the first place, the action of the moon alone, on the earth with its oceans, lakes, and rivers, we perceive that it must tend to equalise the periods of the earth's rotation about its axis, and of the revolution of the two bodies about their centre of inertia; because as long as these periods differ, the tidal action of the earth's surface must keep subtracting energy from their motions. To view the subject more in detail, and, at the same time, to avoid unnecessary complications, let us suppose the moon to be a uniform spherical body, the mutual action and reaction of gravitation between her mass and the earth's will be equivalent to a single force in some line through her centre; and must be such as to impede the earth's rotation as long as this is performed in a shorter period than the moon's motion round the earth. It must, therefore, lie in some such direction as the line MQ in the diagram, which represents, necessarily with enormous exaggeration, its deviation, OQ, from the earth's centre. Now the actual force on the moon in the line MQ may be regarded as consisting of a force in the line MO towards the earth's centre, sensibly equal in amount to the whole force, and a comparatively very small force in the line MT perpendicular to MO. This latter is very nearly tangential to the moon's path, and is in the direction with her motion. Such a force, if suddenly commencing to act, would, in the first place, increase the moon's velocity; but after a certain time she would have moved so much farther from the earth, in virtue of this acceleration, as to have lost, by moving against the earth's attraction,
as much velocity as she had gained by the tangential accelerating force. The effect of a continued tangential force, acting with the motion, but so small in amount as to make only a small deviation at any moment from the circular form of the orbit, is to gradually increase the distance from the central body, and to cause as much again as its own amount of work to be done against the attraction of the central mass, by the kinetic energy of motion lost. The circumstances will be readily understood by considering this motion round the central body in a very gradual spiral path tending outwards. Provided the law of force is the inverse square of the distance, the tangential component of gravity against the motion will be twice as great as the disturbing tangential force in the direction with the motion; and therefore one-half of the amount of work done against the former, is done by the latter, and the other half by kinetic energy taken from the motion. The integral effect on the moon's motion, of the particular disturbing cause now under consideration, is most easily found by using the principle of moments of momenta. Thus we see that as much moment of momentum is gained in any time by the motions of the centres of inertia, of the moon and earth relatively to their common centre of inertia, as is lost by the earth's rotation about its axis. The sum of the moments of momentum of the centres of inertia of the moon and earth as moving at present, is about 4.45 times the present moment of momentum of the earth's rotation.
The average plane of the former is the ecliptic; and therefore the axes of the two moments are inclined to one another at the average angle of 23° 27.5', which, as we are neglecting the sun's influence on the plane of the moon's motion, may be taken as the actual inclination of the two axes at present. The resultant, or whole moment of momentum, is therefore 5.38 times that of the earth's present rotation, and its axis is inclined 19° 13' to the axis of the earth. Hence the ultimate tendency of the tides is to reduce the earth and moon to a simple uniform rotation with this resultant moment round this resultant axis, as if they were two parts of one rigid body: in which condition the moon's distance would be increased (approximately) in the ratio 1:1.46, being the ratio of the square of the present moment of momentum of the centres of inertia to the square of the whole moment of momentum; and the period of revolution in the ratio 1:1.77, being that of the cubes of the same quantities. The distance would therefore be increased to 847,100 miles, and the period lengthened to 48.36 days. Were there no other body in the universe but the earth and the moon, these two bodies might go on moving thus for ever, in circular orbits round their common centre of inertia, and the earth rotating about its axis in the same period, so as always to turn the same face to the moon, and, therefore, to have all the liquids at its surface at rest relatively to the solid. But the existence of the sun would prevent any such state of things from being permanent. There would be solar tides – twice high water and twice low water – in the period of the earth's revolution relatively to the sun (that is to say, twice in the solar day, or, which would be the same thing, the month). This could not go on without loss of energy by fluid friction. It is not easy to trace the whole course of the disturbance in the earth's and moon's motions which this cause would produce, but its ultimate effect must be to bring the earth, moon, and sun to rotate round their common centre of inertia, like parts of one rigid body."[1]
Kant, in 1754, was the first to put forward the view that the rotation of the earth is retarded by tidal friction and that this effect will only reach its conclusion "when its (the earth's) surface will be at relative rest in relation to the moon, i.e. when it will rotate on its axis in the same period that the moon takes to revolve round the earth, and consequently will always turn the same side to the latter." He held the view that this retardation had its origin in tidal friction alone, arising, therefore, from the presence of fluid masses on the earth:
"If the earth were a quite solid mass without any fluid, neither the attraction of the sun nor of the moon would do anything to alter its free axial rotation; for it draws with equal force both the eastern and western parts of the terrestrial sphere and so does not cause any inclination either to the one or to the other side; consequently it allows the earth full freedom to continue this rotation unhindered as if there were no external influence on it."
Kant could rest content with this result. All scientific pre-requisites were lacking at that time for penetrating deeper into the effect of the moon on the rotation of the earth. Indeed, it required almost a hundred years before Kant's theory obtained general recognition, and still longer before it was discovered that the ebb and flow of the tides are only the visible aspect of the effect exercised by the attraction of the sun and moon on the rotation of the earth.
This more general conception of the matter is just that which has been developed by Thomson and Tait. The attraction of the moon and sun affects not only the fluids of the terrestrial body or its surface, but the whole mass of the earth in general in a manner that hinders the rotation of the earth. As long as the period of the earth's rotation does not coincide with the period of the moon's revolution round the earth, so long the attraction of the moon – to deal with this alone first of all – has the effect of bringing the two periods closer and closer together. If the rotational period of the (relative) central body were longer than the period of revolution of. the satellite, the former would be gradually lengthened; [2] if it were shorter, as is the case for the earth, it would be slowed down. But neither in the one case will kinetic energy be created out of nothing, nor in the other will it be annihilated. In the first case, the satellite would approach closer to the central body and shorten its period of revolution, in the second it would increase its distance from it and acquire a longer period of revolution. In the first case, the satellite by approaching the central body loses exactly as much potential energy as the central body gains in kinetic energy from the accelerated rotation; in the second case the satellite, by increasing its distance gains exactly the same amount of potential energy as the central body loses in kinetic energy of rotation. The total amount of dynamic energy, potential and kinetic, present in the earth-moon system remains the same; the system is fully conservative.[3]
It is seen that this theory is entirely independent of the physico-chemical constitution of the bodies concerned. It is derived from the general laws of motion of free heavenly bodies, the connection between them being produced by attraction in proportion to their masses and inverse proportion to the square of the distances between them. The theory has obviously arisen as a generalisation of Kant's theory of tidal friction, and is even presented here by Thomson and Tait as its substantiation on mathematical lines. But in reality – and remarkably enough the authors have simply no inkling of this – in reality it excludes the special case of tidal friction.
Friction is hindrance to the motion of mass, and for centuries it was regarded as the destruction of such motion, and therefore of kinetic energy. We now know that friction and impact are the two forms in which kinetic energy is converted into molecular energy, into heat. In all friction, therefore, kinetic energy as such is lost in order to re-appear, not as potential energy in the sense of dynamics, but as molecular motion in the definite form of heat. The kinetic energy lost by friction is, therefore, in the first place really lost for the dynamic aspects of the system concerned. It can only become dynamically effective again if it is re-converted from the form of heat into kinetic energy.
How then does the matter stand in the case of tidal friction? It is obvious that here also the whole of the kinetic energy communicated to the masses of water on the earth's surface by lunar attraction is converted into heat, whether by friction of the water particles among themselves in virtue of the viscosity of the water, or by friction at the rigid surface of the earth and the comminution of rocks which stand up against the tidal motion. Of this heat there is re-converted into kinetic energy only the infinitesimally small part that contributes to evaporation at the surface of the water. But even this infinitesimally small amount of kinetic energy, leaving the total system earth-moon at a part of the earth's surface, remains first of all subject to the conditions prevailing at the earth's surface, and these conditions lead to all energy active there reaching one and the same final destiny: final conversion into heat and radiation into space.
Consequently, to the extent that tidal friction indisputably acts in an impeding manner on the rotation of the earth, the kinetic energy used for this purpose is absolutely lost to the dynamic system earth-moon. It can therefore not re-appear within this system as dynamic potential energy. In other words, of the kinetic energy expended in impeding the earth's rotation by means of the attraction of the moon, only that part that acts on the solid mass of the earth's body can entirely re-appear as dynamic potential energy, and hence be compensated for by a corresponding increase of the distance of the moon. On the other hand, the part that acts on the fluid masses of the earth can do so only in so far as it does not set these masses themselves into a motion opposite in direction to that of the earth's rotation, for such a motion is wholly converted into heat and is finally lost to the system by radiation.
What holds good for tidal friction at the surface of the earth is equally valid for the so often hypothetically assumed tidal friction of a supposed fluid nucleus of the earth's interior.
The most peculiar part of the matter is that Thomson and Tait do not notice that in order to establish the theory of tidal friction they are putting forward a theory that proceeds from the tacit assumption that the earth is an entirely rigid body,[4] and so exclude any possibility of tidal flow and hence also of tidal friction.
Notes
[1] This theory has since been greatly developed, and the actual rate at which tidal friction is lengthening the day has been approximately found.
[2] A slip of the pen; the word should obviously be "shortened."
[3] There can be no doubt that Engels was right when he pointed out Thomson and Tait's error in saying that the changes in the length of the day and month "could not go on without loss of energy by fluid friction." We now know that there are tides in the earth as well as in the ocean. But Engels was wrong in supposing that the moon could move away from the earth without loss of energy. For in a system such as the earth and moon the angular momentum (moment of momentum) remains constant unless it is diminished or increased by the tidal action of some external body. If both momentum and energy are conserved no systematic slowing down can occur. This is readily seen in the simplified case where the moon is supposed to go round in a circle in the plane of the earth's equator. In this case there are only two possible variables, the lengths of the day and month. But so long as the moment of momentum and the energy of the system are unchanged we have two equations to determine these quantities, and they are therefore fixed.
[4] Although Engels formulated his criticism of Thomson and Tait incorrectly, he was right in a fundamental point. The earth-moon system would evolve in such a way as to lengthen the day and month even if there were no ocean. For the earth is a solid (fester) body, but not a rigid (starrer) body in the sense in which this latter word is used in theoretical mechanics, that is to say a body whose shape is unaltered by the forces on it. Of course a rigid body is a mathematical abstraction, like a flat surface. There are no perfectly rigid bodies nor flat surfaces. And it has now been shown that the solid earth bends slightly as the moon's attraction varies. There are solid tides as well as liquid tides though much smaller. These act in the same way as the tides in the ocean, though much more slowly.


 as much velocity as she had gained by the tangential accelerating force. The effect of a continued tangential force, acting with the motion, but so small in amount as to make only a small deviation at any moment from the circular form of the orbit, is to gradually increase the distance from the central body, and to cause as much again as its own amount of work to be done against the attraction of the central mass, by the kinetic energy of motion lost. The circumstances will be readily understood by considering this motion round the central body in a very gradual spiral path tending outwards. Provided the law of force is the inverse square of the distance, the tangential component of gravity against the motion will be twice as great as the disturbing tangential force in the direction with the motion; and therefore one-half of the amount of work done against the former, is done by the latter, and the other half by kinetic energy taken from the motion. The integral effect on the moon's motion, of the particular disturbing cause now under consideration, is most easily found by using the principle of moments of momenta. Thus we see that as much moment of momentum is gained in any time by the motions of the centres of inertia, of the moon and earth relatively to their common centre of inertia, as is lost by the earth's rotation about its axis. The sum of the moments of momentum of the centres of inertia of the moon and earth as moving at present, is about 4.45 times the present moment of momentum of the earth's rotation.
as much velocity as she had gained by the tangential accelerating force. The effect of a continued tangential force, acting with the motion, but so small in amount as to make only a small deviation at any moment from the circular form of the orbit, is to gradually increase the distance from the central body, and to cause as much again as its own amount of work to be done against the attraction of the central mass, by the kinetic energy of motion lost. The circumstances will be readily understood by considering this motion round the central body in a very gradual spiral path tending outwards. Provided the law of force is the inverse square of the distance, the tangential component of gravity against the motion will be twice as great as the disturbing tangential force in the direction with the motion; and therefore one-half of the amount of work done against the former, is done by the latter, and the other half by kinetic energy taken from the motion. The integral effect on the moon's motion, of the particular disturbing cause now under consideration, is most easily found by using the principle of moments of momenta. Thus we see that as much moment of momentum is gained in any time by the motions of the centres of inertia, of the moon and earth relatively to their common centre of inertia, as is lost by the earth's rotation about its axis. The sum of the moments of momentum of the centres of inertia of the moon and earth as moving at present, is about 4.45 times the present moment of momentum of the earth's rotation.